notion으로 보면 더 편합니다.
www.notion.so/Batch-Normalization-0649da054353471397e97296d6564298
Batch Normalization
Summary
www.notion.so
목차
- Summary
- Introduction
- Background
- Normalization
- Covariate Shift
- Batch Normalization
- Algorithm
- Learnable Parameter gamma, beta
- Inference with Batch Normalization
- 모집단 추정방식
- Moving average 방식
- Undertstanding Batch Normalization
- BN이 ICS를 제거하는가?
- 왜 성능이 좋은가?
- Optimization Landscape
- Lipschitz
- 사족들
- Reference
Summary
- 역할
- 각 레이어의 입력 feature의 분포를 re-centering & re-scaling
- 장점 → 경험적으로 높은 성능을 낸다고 널리 알려져 있음 & 이유에 대해서는 아직도 연구 진행중
- Faster training (learning rate 를 더 높게 설정할 수 있음)
- Stable training (less vanishing & exploding gradients)
- Regularization (less overfitting, more generalized)
- 단점
- 큰 mini-batch size 필요 → Mini-batch가 전체 dataset과 비슷한 분포를 가져야함.
- RNN에서 사용 불가능
- 잘 동작하는 이유
- 아마도 Internal covariate shift를 제거했기 때문이다.
- 2018 논문: ICS때문은 아니다! 실험적, 수학적으로 증명
- Objective function의 solution space를 smoothing 했기 때문이다.
- ㄱㄱ
- 아마도 Internal covariate shift를 제거했기 때문이다.
Introduction
머신러닝에서 Batch Normalization은 빼놓을 수 없는 주제 중 하나이다. 많은 네트워크들이 관습적으로 Batch Normalization을 자신들의 연구에 끼얹어 보고는 하는데 오늘은 이 Batch Normalization에 대해서 알아보고, 그와 관련된 개념들을 정리해보고자 한다.
Batch Normalization (BN)은 처음 2015년도에 네트워크상의 Internal covariate shift(ICS)를 제거하기 위한 목적으로 제안되었다. 거의 대부분의 네트워크에 BN을 추가했을 때, 추가하지않았을 때보다 굉장히 빠른속도로, 안정적이게 학습을 수행할수 있다는 사실이 실험적으로 밝혀졌었다. 하지만 2018년도에 그 이유가 ICS를 제거했기 때문이 아니라 그저 solution space를 smoothing 했기 때문이라는 주장이 제안되었고, 실험적, 수학적으로 이것이 사실이라고 밝혀졌다.
BN은 크게 3가지 장점이 있다.
- 네트워크를 vashing & exploding gradient를 감소시키고 안정적으로 학습시킬 수 있도록 도와준다.
- 또한, overfitting을 감소시키며 네트워크가 더 쉽게 generalize 할수 있다. 즉, Reglarization 효과를 가진다.
- 이 덕분에 높은 learning rate로 학습을 시킬 수 있으며, 이는 학습을 빠르게 convergence에 이를 수 있게 만들어준다.
- 하지만, 이러한 BN에도 몇가지 단점들이 있다.
- 일반적으로 머신러닝을 수행할 때, 한꺼번에 데이터셋 전체를 학습 시킬 수 없어서 작은 mini-batch단위로 학습을 시킨다. BN은 mini-batch 단위로 Normalization을 수행하기 때문에 mini-batch size가 성능에 영향을 준다. 구체적으로는 큰 mini-batch ize를 필요로 한다. 그 이유는 Mini-batch가 전체 dataset와 비슷한 분포를 가져야 하기 때문이다. (어쨌든 mini-batch도 전체 데이터셋에서 sampling 하는 것이니까 mini-batch에도 먹힌다.)
- 몇가지 네트워크에서는 BN을 사용하기 어렵다. 대표적인 예로 RNN와 같은 sequental 데이터를 처리하는 경우를 들 수 있다.
Background
Normalization
Batch Normalization은 이름에서부터 그렇듯 학습을 수행할 때 Normalization을 수행하는 방식이다. 때문에 이러한 Normalization과 관련된 내용을 알아보고자 한다.
데이터 전처리 중 Normalization의 목적은 모든 Feature들이 동일한 scale을 가지도록 하는 것을 말한다. 여기서 여러가지 Normalization 방식들이 있지만, 가장 유명한 Normalization 방식은 Min-Max와 Standardization이다.
여기서 머신러닝에서 주로 사용되는 Normalization 개념은 Standardization이다.
Standardization
Standardization의 경우, 처리하고자하는 데이터상의 mean과 standard deviation을 구하고, 각 feature data에서 mean을 빼고, standard deviation을 나눠주는 방식으로 shift and scaling을 수행한다.
참고로 머신러닝상에서는 일반적으로 mean와 standard deviation 함수는 각각 $\mu$, $\sigma$로 주로 표현되면, 따라서 새로운 데이터 $x'$는 아래의 식으로 구해진다.
$$x' = \frac{x-\mu(x)}{\sigma(x)}$$
Standardization을 왜 shift and scaling이라고 하는가?
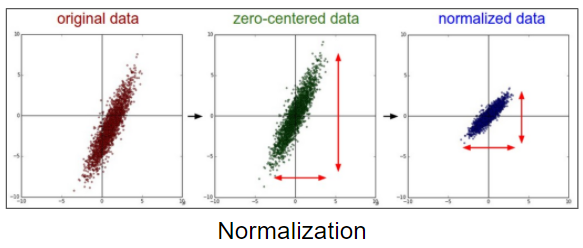
아래의 그림을 보면 직관적으로 알 수 있다. 원본의 데이터 분포가 아래와 같다고 했을 때, $\mu(x)$를 각 데이터에 대해서 빼주었을 때, 아래의 그림의 zero-centered data가 되는데 그 모습이 데이터 전체가 mean을 중심으로 하도록 이동시킨것과 같기 때문에 shift 라고 말한다. scaling은 이 데이터에 대해서 표준 편차로 나눠주게 되는데, 이를 통해서 전체의 퍼져있는 정도를 각 feature (가로, 세로)마다 유사하도록 맞춰주기 때문이다.
Whitening
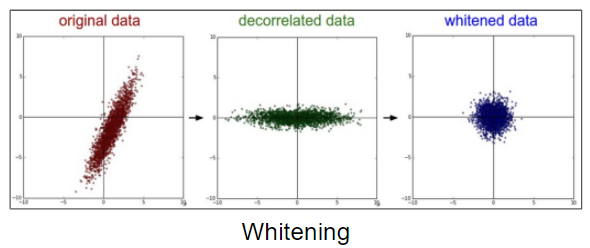
이러한 Standardization 방식보다 더 좋다고 알려진것이 whitening이다. whiteing은 아래의 두가지를 만족시키도록 데이터를 변환시켜준다.
- PCA를 통해서 각 feature들을 재가공한다. 이를 통해서 Feature간의 correlation을 감소시킨다. 즉, 중복(redundant)되는 정보를 제거한다.
- Decorrelated data
- 모든 Feature들이 동일한 scale을 가지도록 한다. (Standadization와 같다)
- whitened data
PCA는 주성분분석이라고해서 각 성분을 분석해서 성분간 중복을 제거해줄 수있는 기술이다. 그리고 이러한 주성분분석은 굉장히 많은 연산량을 요구하는데, 그 때문에 높은 차원, 그리고 많은양의 데이터에 대해서 이러한 주성분 분석을 수행하기에 많은 어려움이 따른다.
그개념을 여기서 설명하기에는 너무 길기 때문에 언젠가 시간이나면 포스팅하도록 하겠다.
PCA는 데이터의 경향성을 찾아서, 새로운 축을 만들어주는 것과 같이 동작하는데, 중간의 그래프가 어떻게 변하는지 위의 standardization과 비교해서 보면 그 차이점을 볼 수 있을 것이다.
Whitening은 여러 논문에서 중간중간에 한번씩 끼얹어보는 방식으로 쓰이는걸 많이 보았다. 머신러닝의 성능향상에 영향을 미친다는 증거로 볼 수 있는데, 여기에 대해서는 완벽히 하는 것이 아니라 다음에 더 조사해보고 추가 포스팅을 하겠다.
Covariate Shift
Corvariate Shift는 대표적으로 어떤 데이터셋을 뽑았을 때, Train 데이터의 분포와 Test 데이터의 분포가 달라서 발생하는 문제이다.
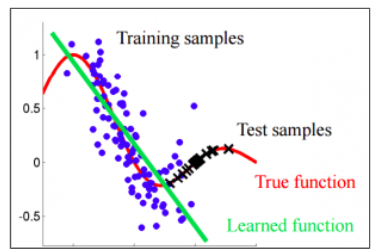
이 그래프를 보자. 실제 데이터의 분포가 빨간색그래프인 True function을 따른다. 그런데 만약 우리가 Train Dataset을 sampling 할 때 파란색 점처럼 샘플링을 했다고 해보자. 그러면 네트워크를 녹색의 Learned function처럼 학습을 수행할 것이다. 즉, 실제는 빨간색 그래프인데, 학습된 모델은 녹색그래프처럼 나와서 검은색 데이터, Test Dataset을 제대로 예측하지 못하게 된다. 이를 다르게 말하자면 Train Dataset과 Test Dataset의 분포가 서로 달랐기 때문에 발생한 문제이다.
When the distribution of the inputs used as predictors (독립변수, 예측변수, covariates) changes between training and production stages
Internal Covariate Shift(ICS)는 이러한 Covariate Shift가 Multi layers network에서 각 internal layer들 사이에서도 발생한다는 것이다. 다시말해보자면, 각 layer에서 받아들이는 input의 분포가 학습 과정중 계속 변함으로 input으로 이전과 전혀다른 분포가 들어왔을 때, 잘 학습을 못하게 만들 수 있다는 것이다.
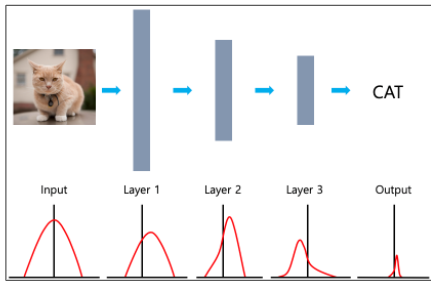
layer 1의 output은 layer2의 인풋이 된다. layer2의 아웃풋은 layer3의 인풋이 된다. multi layers network의 경우 위와같이 한 레이어들의 output들이 다른 레이어의 인풋으로 들어가게 된다. 이 때, 학습 과정에서 layer2의 분포가 갑자기 이전과 다른 형태의 분포로 변한다면 layer3는 전혀 다른 분포가 들어왔기 때문에 마치 covariate shift의 결과처럼 네트워크가 정확한 True Function을 예측하는데 방해가 될 것이라고 생각한 것이다.
Purposed Method (Batch Normalization)
이러한 ICS를 제거하기 위해서 각 레이어를 거칠 때마다 데이터의 분포를 standardization 시켜주는 Batch Normalization을 제안했다.
Algorithm
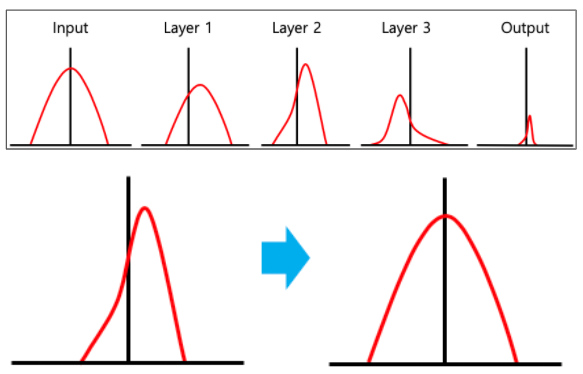
저 파랑색 화살표가 바로 Batch Normalization이다. 이러한 Batch Normalization은 Activation 을 거치기 전에 적용되게 되는데, 논문에서는 아래와 같은 알고리즘으로 기술되어 있다.

간단히 알고리즘을 풀어보잠녀 어떤 mini-batch의 사이즈가 m인 데이터 $x$들을 받았을 때,
mini-batch의 mean을 구하고,
$$\mu_{\mathcal{B}} \leftarrow \frac{1}{m} \sum_{i=1}^{m} x_{i}$$
variance를 구해서
$$\sigma_{\mathcal{B}}^{2} \leftarrow \frac{1}{m} \sum_{i=1}^{m}\left(x_{i}-\mu_{\mathcal{B}}\right)^{2}$$
normalization 해준다.
$$\widehat{x}_{i} \leftarrow \frac{x_{i}-\mu_{\mathcal{B}}}{\sqrt{\sigma_{\mathcal{B}}^{2}+\epsilon}}$$
그런데 저기 이상한게 들어가 있다. 바로 $\epsilon$이거 . 이건 그냥 아주 작은 값을 가지는 상수라고 보면 된다. 왜냐면 표준편차가 0이 되면 무한대로가버리기 떄문에 이를 방지하기 위해서 저렇게 입실론을 더해주는 방식으로 구현한다.
그런데 그다음에 이상한 게 하나 더있다. 바로 learned parameter $\gamma, \beta$
Learnable parameter $\gamma, \beta$
BN은 Activation Layer 이전에 위치한다. 때문에 Normalization을 수행함으로서 Activation Layer의 non-linearity를 감소시킬 수 있다는 우려가 있다.
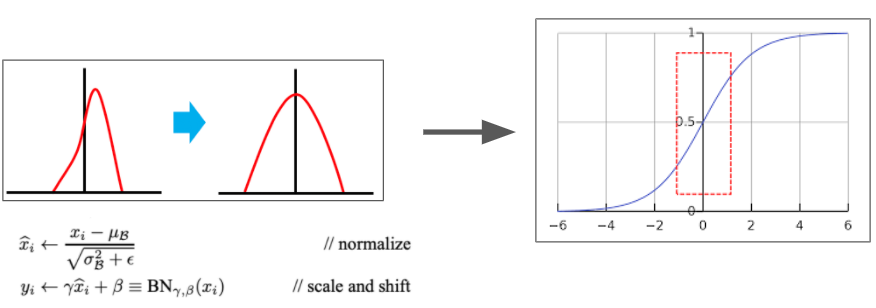
Normalizaation을 거치고 그대로 Actication layer (tanh)의 input으로 사용할 경우, 정의역이 대부분 빨간색 점선 박스 쪽으로 이동할 것이다. 그리고 그래프에서 보면 알겠지만 해당 정의역에서의 Activation Function Graph의 모양이 매우 linear한 성질을 띄는데 이럴 경우 non-linearity가 떨어진다는 문제가 발생하는 것이다. (이게 왜문제인지 모른다면? ⇒ activation 파트를 다시 공부하고 오자. 이것도 곧 포스팅할 예정...)
따라서 Non-linearity를 높이기 위해서 데이터의 분포를 적절하게 scale & shift를 시킨다.
$$y_{i} \leftarrow \gamma \widehat{x}_{i}+\beta \equiv \mathrm{B} \mathrm{N}_{\gamma, \beta}\left(x_{i}\right)$$
scale 해주는 것이 $\gamma$이고, shifting 해주는 것이 $\beta$다.
Inference with Batch Normalization
이제 학습을 완료했다. 그런데 문제가 하나가 있는게, 학습이 끝난 시점, 즉 production 시점에서 더이상 mini-batch의 mean & standard deviation 을 쓸 수 없다는 것이다. (학습할 때 무엇으로 평균을 쓸 것인가?...)
따라서 mini-batch의 mean & standard deviation을 대체할 방법이 필요한데 이 때 크게 2가지 방식이 있는데, 둘 모두 Training set의 mean & standard deviation을 사용해서 유도한다.
모집단 추정방식
고등학생때 한번쯤 해봤을 것이다! 신승범 선생님께서 (m-1)이 그냥 좋다고 했던 기억이 있다...
$$E\left[x^{(k)}\right]=E_{B}\left[\mu_{B}^{(k)}\right]$$
$$\operatorname{Var}\left[x^{(k)}\right]=\frac{m}{m-1} E_{B}\left[\sigma_{B}^{(k)^{2}}\right]$$
Moving average 방식
$$\begin{array}{l}\hat{\mu} \leftarrow \alpha \hat{\mu}+(1-\alpha) \mu_{\mathcal{B}}^{(i)} \\hat{\sigma} \leftarrow \alpha \hat{\sigma}+(1-\alpha) \sigma_{\mathcal{B}}^{(i)}\end{array}$$
디테일한 설명은 생략하겠다. 모집단 추정방식은 학습 시에 평균과 분산들을 모두 기억하고 있어야 하기 때문에 비효율적이고, 주로 Moving average 방식으로 구현된다고 한다.
시간이 나면 한번 다뤄보도록하겠다. 그런데 날지모르겠네...
Understanding Batch Normalization
이 이후부터는 How Does Batch Normalization Help Optimization 논문의 내용이다.
일단 확실히 BN이 성능하나는 훌륭하다. 하지만 여전히 BN paper의 ICS가 제거되었는지 명확한 실험 및 수학적 설명이 부족하다는 것이다. 그리고 아래와 같은 결론을 내었다.
- BN은 ICS를 제거하지 않는다.
- ICS가 있다고 하더라도 학습에 나쁜영향을 주지 않는다.
- BN이 성능이 좋은 이유는 solution space를 smoothing 했기 때문이고, 이는 다른 방식으로도 같은 효과를 얻을 수 있다.
- 대표적인 다른방식에는 dropout과 같은 방법들이 있으며, regluarization 등도 이에 해당될 것이다.
BN이 ICS를 제거하는가?
저자는 VGG네트워크를 VGG without BN , VGG + BN , VGG + BN + Noise 로 나누어 실험을 수행한다.

그래프가 난해하다. depth 축은 학습의 진행도(step? 명시안되어있는 것 같다 time이라고 써져있던데)이고, 하나의 슬라이스가 분포도를 나타내는 것으로 보인다. 여기서 주목할만한 것은 BN을 적용시킨 것이 더 ICS가 높다는 것이다. (각 스텝별로 데이터의 분포가 확실히 다르다. 즉 ICS가 발생한 것이다) 그럼에도 불구하고 아래와 같은 실험 결과가 나왔다.
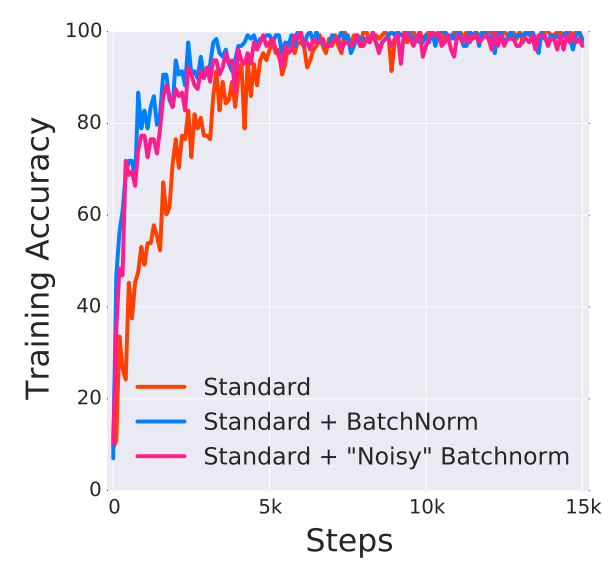
즉 VGG를 그냥 사용한 것이 가장 성능이 안좋았으며, VGG+BN+Noise가 그다음으로 좋았고, 역시 VGG+BN을 사용한것이 가장 좋았다. 주목할만한 것은 Noise를 추가해서 ICS를 추가적으로 일으켰음에도 불구하고, BN없이 사용한 VGG보다 성능이 좋았으며, 이는 ICS가 학습의 성능에 큰영향을 주지 못한다는 반증이다.
그렇다면 왜 성능이 좋은가?
Optimization landscape
바로 solution space를 smoothing 하기 때문이라는 것이다.
BN은 Loss function의 Lipschitzness를 impove하는데, 이는 Gradient가 stable하게 감소할수 있도록 만들어 준다. 즉 high learning rate에서도 stsable하게 learning하도록 만들어준다. 즉 soulution space를 아래와 같이 smoothing한다!

Lipschitz
Lipschitz 함수란 두 점 사이의 거리가 일정비 이상으로 증가하지 않음. 즉 미분 계수가 상수 K를 넘지 않는 함수다.
인데, Lipschitness를 개선했다는 것은 gradient가 급격히 커지는 것을 방지할수 있다는 것이다.
$$\left|\frac{f(x)-f(y)}{x-y}\right|<=K$$

위 처럼 loss가 안정적으로 줄어들고, Gradient predictiveness또한 좋아졌다. (gradient의 방향성? 정도? 그런의미인듯 정확히는 모르겟따)
수학수학한건 다루지 않는다.
사족들
일반적으로 tensorflow의 shape은 BHWC, pytorch는 BCHW다. B는 배치 C는 채널 HW는 Height와 Width다. 이를 수식으로 명식적으로 나타내면
$$\mu_{c}(x)=\frac{1}{N H W} \sum_{n=1}^{N} \sum_{h=1}^{H} \sum_{w=1}^{W} x_{n c h w}$$
$$\sigma_{c}(x)=\sqrt{\frac{1}{N H W} \sum_{n=1}^{N} \sum_{h=1}^{H} \sum_{w=1}^{W}\left(x_{n c h w}-\mu_{c}(x)\right)^{2}+\epsilon}$$
$$\mathrm{BN}(x)=\gamma\left(\frac{x-\mu(x)}{\sigma(x)}\right)+\beta$$
이렇게 될 것이다. 보면 group-by C인것을 알수있다. 왜 group by C인가? 에대해서 한번쯤 생각해보는 시간이 있었는데, 사실좀만 생각해보면 당연한 것이다.
우리가 채널이라고 부르는 것은 사실 서로다른 feature들이다. 매우 일반적인 경우 0번 채널(feature)는 키, 1번 채널(feature)는 몸무게다. 그럼 당연히 normalization을 수행할 때, 키는 키끼리, 몸무게는 몸무게 끼리 normalization을 수행해야한다. 당연히 채널로 묶어서 normalization을 수행해야하는것이고, BN도 channel로 묶어서 normalization을 수행하는 것이다.
진짜 끝
Reference
Andrew Ng님의 강의자료
Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
'ML > 기초 이론' 카테고리의 다른 글
| Entropy, Cross Entropy, KL-Divergence에 대해 알아보자 (5) | 2021.02.06 |
|---|
