자 다시 GAN 포스팅을 작성할 시간이네요.
아 GAN은 쓸게 많아서 너무 괴로워요... PS쪽이 확실히 더 작성하기 편하네요.
익숙한 개념이라서 그런걸까요?
오늘 알아볼 내용은 GAN의 증명과 한계 그리고 해결법에 관한 내용입니다. 오늘 내용은 WGAN을 들어가기 앞서 필요한 GAN에 대한 증명과 한계들을 다뤄볼 예정입니다.
수학적인 내용을 최소한으로 준비했지만, 도저히 못덜어낸 수학들이 좀 많이 남았습니다.
작성한 글에 오류가 있다면 코멘트 달아주세요! 그럼 바로 시작하겠습니다.
복습
역시 복습을 안하고 갈수는 없겠죠?
복습에서는 이전 포스팅의 내용을 요약하도록 하겠습니다.
[논문 정리] GAN에 대해서 알아보자 (1) - 개념, 알고리즘, 소스코드 분석
GAN에 대해서 알아보자 - 개념, 알고리즘, 소스코드 최근에 GAN에 관해서 이것저것 많이 찾아볼 기회가 있어서 이것을 정리하고 블로깅하고자 합니다. 이번 블로깅에서는 최대한 수학적인 내용없
lifeignite.tistory.com
GAN의 Component
GAN은 두가지 component로 구성되어 있습니다. Generator와 Discriminator입니다. Generator는 실제 데이터와 유사한 분포의 데이터를 생성하기 위해 노력하는 Component죠. Discriminator는 Generator가 만든 가짜 데이터와 실제 Data를 구별해주는 Component였습니다. Discriminator로 머신러닝 네트워크를 사용하는 이유는 generator가 생성하는 분포와 실제 데이터 분포를 수식화 하기 힘든 매우 어려운 분포이기 때문입니다.
GAN의 Sampling
그리고, GAN은 latent space에서 latent vector z를 sampling합니다. 초기의 latent space는 아무런 의미를 가지지 않기 때문에 여기서 sampling된 latent vector z도 아무런 의미를 가지지 않습니다만, 학습을 통해서 latent vector와 특정 데이터를 연결하게 되면서 latent space가 의미를 가지도록 바꿔줍니다. 마치 사람들이 아무의미없는 것들에 의미를 부여하는것처럼 네트워크도 경험적으로 latent space에 의미를 부여하기 시작할겁니다. ㅎㅎ
GAN의 학습 Algorithm
GAN의 학습은 2가지 step으로 이루어졌었죠. 첫번째 스텝에서는 Generator를 고정시키고, Discriminator를 학습시킵니다. 두번째 스텝에서는 Discriminator를 고정시키고, Generator를 학습시킵니다. 그리고 고정시킴에 따라 Loss Function이 일부 변경되었었습니다.
전체를 요약해보자면
GAN의 전체 구조를 요약해보자면 GAN은 latent space에서 sampling 한 z로부터 Generator는 어떠한 데이터 분포를 만듭니다. 그리고 이렇게 생성한 Generator의 분포와 실제 데이터 분포를 Discriminator로부터 비교하게 함으로서 G가 잘생성하면 D를 혼내주고, D가 잘 구분하면 G를 혼내주는 방법으로 학습을 수행합니다.
아래와같은 구조를 가지고 있죠.
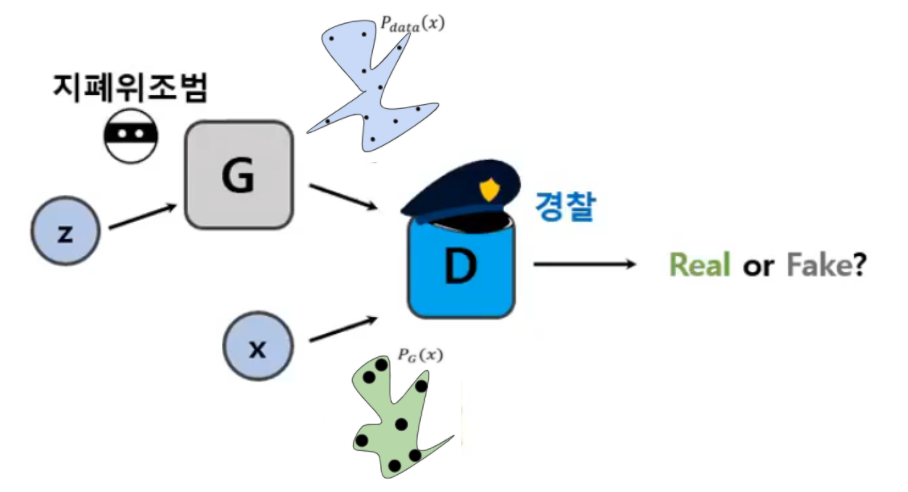
GAN과 JS Divergence
직관적으로 GAN이 왜 동작하는지는 쉽게 이해가 됩니다. 그런데 직관적으로만 ㅇㅋ 하고 가면 조금 찝찝하죠. 그래서 GAN이 동작하는 이유에 대해서 증명을 하나하고 넘어가겠습니다.
이 내용은 이 후 WGAN으로 넘어가기 위해서 반드시 필요하다고 생각해서 넣었는데, 생략하시고 싶으시면 바로 WGAN으로 넘어가시면 됩니다.
한줄 요약
최초 제안된 GAN의 Loss function은 JSD를 계산하게 되는데, JSD는 두 분포가 겹치지 않았을 때, 상수 값을 가져서 gradient 계산으로 optimal을 찾는 것이 쉽지 않다.
GAN의 동작 조건
GAN의 목표는 실제 데이터 분포인 $P_{data}$ 와 Generator 가 만든 가짜 데이터 분포인 $P_{g}$ 가 같아지는 것을 목표로 합니다.
즉 GAN의 Loss Function인 아래 식이 최적일 때, $P_{data}=P_g$ 임을 만족해야한다는 뜻이죠.
$$\min_{G} \max_{D} V(G, D)=\mathbb{E}_{x \sim P_{data}(x)}[\log D(x)]+\mathbb{E}_{z \sim P_{z} (z)}[\log (1-D(G(z))]$$
일단, 최적의 G에 대해서 생각할 거니까, G를 고정한 것과 같죠? 저번 시간에 봤던 식이 튀어나올 겁니다.
$$\max_{D} V(G, D)=\mathbb{E}_{x \sim P_{data}(x)}[\log D(x)]+\mathbb{E}_{x \sim P_g (x)}[\log (1-D(x)]$$
Term 정리
자 변수가 너무 많으니까 좀 정리해볼께요.
- $x$: 이미지 ( high-dimensional vector)
- $G$: generator 함수입니다.
- $D$: discriminator 함수입니다.
- $P_{data}$: 실제 데이터 셋의 분포입니다.
- $P_g$: generator가 생성한 가짜 데이터의 분포입니다.
- $\mathbb{E}$: 기대값이에요. 의외로 이 기호를 잘모르시는 분들이 많더라구요.
- 기대값은 $p(x)$의 확률로 나타나는 어떤 함수 $f(x)$의 평균으로써 $$\mathbb{E}_{x \sim p}[f] = \int p(x)f(x)dx$$로 계산될 수 있습니다.
Loss Function 이 최적일 때의 D
자 변수를 정리해놓고 봤는데, 저희의 목적을 잊지 말죠.
저희가 확인하고 싶은 것은 이 Loss Function이 최적일 때, $P_{data}=P_g$ 가 되는지 확인하는 것이에요.
그럼, Loss Function이 최적일 때는 어떨까요? 바로 Loss Function $V$ 를 최대화하는 것입니다.
Loss Function을 최대화하는 최적의 (optimal) $D$를 $D^*$ 라고 할께요 . 이를 수식으로 나타내면 아래와 같은 거에요.
$$D^*=arg\underset {D}{\max}V(D,G)$$
그리고 우리의 Loss Function $V$의 식이 아래와 같았습니다.
$$\max_{D} V(G, D)=\mathbb{E}_{x \sim P_{data}(x)}[\log D(x)]+\mathbb{E}_{x \sim P_g (x)}[\log (1-D(x)]$$
$\mathbb{E}$ 를 풀어볼게요. 기대값은 $\mathbb{E}_{x \sim p}[f] = \int p(x)f(x)dx$ 로 풀리니까,
$$\begin{aligned}V &=\mathbb{E}_{x \sim P_{ data }}[\log D(x)]+\mathbb{E}_{x \sim P_{g}}[\log (1-D(x))] \\&=\int_{x} P_{data }(x) \log D(x) d x+\int_{x} P_{g}(x) \log (1-D(x)) d x \\&=\int_x\left[P_{\text {data }}(x) \log D(x)+P_{g}(x) \log (1-D(x))\right] d x\end{aligned}$$
단순하게 식에 대입하고, 적분 기호안쪽으로 모아둔 것 밖에 없는 식입니다! 정말 단순한 식이에요.
자 이제 저 식에서 $a=P_{data}$ 이고, $b=P_G(x)$ 라고 했을 때 위식을 정리해보면,
$$f(x) = alogx+blog(1-x)$$
꼴이 되게 됩니다. 이 함수를 그래프로 그려보시면, 위로 볼록한 모양이 되게 되는데, 0과 1 사이에서 미분 가능합니다. 저희는 이 식의 최대값을 구하고 싶은 거니까 이 식을 미분해볼께요.
그러면 아래와 같이 미분이 가능합니다. (고등학교 로그 미분 입니다!)
$$\begin{aligned} \frac{f(x)}{dx} = \frac{a}{x} - \frac{b}{1-x}&=0 \\ a(x-1)+bx &=0\\ (b+a)x-a &=0 \\ \therefore x =\frac{a}{a+b} \\ \end{aligned}$$
즉, $x$가 $\frac{a}{a+b}$ 일 때, 최대 값을 가진다는 뜻이죠.
최적의 D에 다시 $a=P_{data}$ 이고, $b=P_G(x)$ 를 넣고 정리해보자면,
$$optimal \space D^*= \frac{P_{data}(x)}{P_{data}(x)+P_G(x)}$$
이 되게 됩니다.
D가 최적일 때, Loss Function의 의미는?
그럼 $D^*$ 일 때, 식은 어떻게 될까요?
한번 $a=P_{data}$ 이고, $b=P_G(x)$ , $D^*=\frac{a}{a+b}$ 로 넣고 정리 해볼께요.
$$\begin{aligned} &\max _{D} V(G, D)=V\left(G, D^{*}\right) \\ &=\int_x\left[P_{\text {data }}(x) \log D^*(x)+P_{G}(x) \log (1-D^*(x))\right] dx\\&=\int_x[\text{log}(a\frac{a}{a+b}) + \text{log}(b(1-\frac{a}{a+b}))]dx \\&=\int_x[\text{log}(\frac{1}{2}a\frac{a}{(a+b)/2}) + \text{log}(\frac{1}{2}b\frac{b}{(a+b)/2})]dx\\&=-2\text{log}2 + \int_x\text{log}a\frac{a}{(a+b)/2}dx + \int_x\text{log}b\frac{b}{(a+b)/2}dx \end{aligned}$$
자! 여기서 KLD와 JSD가 등장하게 됩니다. KLD에 대해서는 아래 포스팅을 참고하세요!
Entropy, Cross Entropy, KL-Divergence에 대해 알아보자
Entropy 엔트로피는 머신러닝에서 정보량을 나타내는 방법으로 사용된다. 정보의 량이라는게 되게 추상적으로 들리는데, 생각해보면 되게 간단한 개념이다. ML상에서 굉장히 많이 사용되는 개념
lifeignite.tistory.com
어쨌든 KL Divergence는 아래와 같이 정의됩니다.
$$KL(P \parallel Q)= \sum_xP(x)log\frac{P(x)}{Q(x)}$$
이식을 사용해서 풀어보자면,
$$\max _{D} V(G, D)=V\left(G, D^{*}\right) \\ =-2\text{log}2 + \int_x\text{log}a\frac{a}{(a+b)/2}dx + \int_x\text{log}b\frac{b}{(a+b)/2}dx\\ =-2 \log 2+\int_{x} P_{\text {data }}(x) \log \frac{P_{\text {data }}(x)}{\left(P_{\text {data }}(x)+P_{G}(x)\right) / 2} d x \\ +\int_{x} P_{G}(x) \log \frac{P_{G}(x)}{\left(P_{\text {data }}(x)+P_{G}(x)\right) / 2} d x \\ =-2 \log 2+\mathrm{KL}\left(\mathrm{P}_{\text {data }} \| \frac{\mathrm{P}_{\text {data }}+\mathrm{P}_{\mathrm{G}}}{2}\right)+\mathrm{KL}\left(\mathrm{P}_{\mathrm{G}} \| \frac{\mathrm{P}_{\text {data }}+\mathrm{P}_{\mathrm{G}}}{2}\right)$$
그리고, Jensen-Shannon Divergence(JSD)는 아래와 같이 정의가 됩니다.
$$\begin{aligned}\operatorname{JSD}(P \| Q)=\frac{1}{2} KL(P \| M) &+\frac{1}{2} KL(Q \| M) \\M &=\frac{1}{2}(P+Q)\end{aligned}$$
JSD는 KL의 개량형 버전이라고 생각하셔도되는데, KL이 대칭성이 성립하지 않아 거리로 사용할 수 없던 것을 대칭적으로 만들어줘 거리로 사용할 수 있게 됩니다.
모양이 JSD 처럼 변했죠? 그럼 아래와 같이 정리 할수 있게 됩니다.
$$\max _{D} V(G, D)=V\left(G, D^{*}\right)\\=-2 \log 2+\mathrm{KL}\left(\mathrm{P}_{\text {data }} \| \frac{\mathrm{P}_{\text {data }}+\mathrm{P}_{\mathrm{G}}}{2}\right)+\mathrm{KL}\left(\mathrm{P}_{\mathrm{G}} \| \frac{\mathrm{P}_{\text {data }}+\mathrm{P}_{\mathrm{G}}}{2}\right) \\=-2 \log 2+2 J S D\left(P_{\text {data }} \| P_{G}\right)$$
오우 정신 사납습니다. 결론은 저희의 Loss function은 JSD로 귀결되게 됩니다.
그리고 JSD는 두 분포사이의 거리로 사용할 수 있음으로, 따라서 위의 수식을 최소로 만드는 것은 두 분포사이의 거리를 최소로 만드는 것이란 거죠!
WGAN의 등장
자 이제부터 쉬워져요. 왜냐면 여기서 수학을 다뺏거든요.
한숨돌리시고 갑시다!
JS Divergence는 학습에 적합하지 않다!
WGAN에서 주장하길 좋은친구아저씨가 제안한 loss의 JSD는 학습에 적합하지 않다는 것이었습니다. 이걸 이해하기 위해서는 SUPP를 이해하셔야하는데, 간단히 설명할께요.
지지 집합 SUPP
SUPP는 support라고 읽는데, 한국어로는 지지집합이라고 합니다. 멋진 위키를 참고하자면
수학에서, 함수의 지지집합(支持集合, 영어: support 서포트[*]) 또는 받침은 그 함수가 0이 아닌 점들의 집합의 폐포이다.
X가 위상 공간이고, ${\displaystyle f\colon X\to \mathbb {R} }$이 함수라고 하자. 그렇다면 ${\displaystyle f}$의 지지집합 ${\displaystyle \operatorname {supp} f}$는 다음과 같다.
${\displaystyle \operatorname {supp} f=\operatorname {cl} {x\in X\colon f(x)\neq 0}}$
여기서 ${\displaystyle \operatorname {cl} }$ 폐포 연산자다.
인데, 사실 어려운말 다 쳐내고, 이해하시면 좋은 것 단하나 바로 0이 아닌 점들의 집합 입니다. 콤펙트하고 머시기하고 유계 집합 머시기 이런것들이 있는데 사실 저도 잘모릅니다. 수학과가아니라서요. 개념상 0이 아닌 점들의 집합으로 이해하고 넘어가셔도 큰문제가 없습니다.
그림으로 표현해보겠습니다. 두 분포 $\mathbb{P}_r$ 과 $\mathbb{P}_g$ 가 있다고 하겠습니다. 그 분포가 아래와 같이 있다고 가정해볼께요.

여기서 $SUPP \space \space \mathbb{P}_r$ 는 B 공간이 되고, $SUPP \space \space \mathbb{P}_g$ 는 A공간이 된다는 겁니다. 그야말로 0이 아닌 점들의 집합입니다.
이 때, $\mathbb{P}_r(A)=0, \mathbb{P}_r (B)=1$ 이 될 것입니다. 반대로, $\mathbb{P}_g(A)=1, \mathbb{P}_g (B)=0$ 이 되겠죠?
분포의 거리 측정
자 그럼 조금더 직관적인 설명을 위해서, 두 확률 변수를 2차원상의 분포라고 가정해서 생각해보겠습니다.

두 분포가 겹치지 않는다는 사실은 명확하죠. 서로 $0$ 과 $\theta$ 사이에서만 움직이니까요.
여기서 $\theta$ 는 다양한 값을 가질 수 있습니다.
하지만, $\theta \neq0$ 인 경우를 제외한 어떤 경우에도 두 분포가 겹칠 수는 없습니다. 이 경우 두 분포 중 하나가 0이 아닌 값을 가질 때는 다른 분포에서는 무조건 0인 값을 가지게 될 것입니다.
식으로 나타내면
$$\left\{\begin{array}{ll}P_{0}(x) \neq 0 & \Rightarrow P_{\theta}(x)=0 \\P_{\theta}(x) \neq 0 & \Rightarrow P_{0}(x)=0\end{array}\right.$$
이 떄 이상적으로 분포의 거리를 측정하는 지표라면 이 때 두 분포사의 거리는 어떻게 측정되는 것이 좋을까요?
직관적으로 두 분포사이의 최단거리(직선거리) $\theta$ 에 따른 값을 가지는 것이 적합할 것입니다. 예를들면 $\text{distance}(\mathbb{P}_0,\mathbb{P}_\theta)=\theta$ 와 같이 나타낼 수 있으면 좋겠네요.
KL의 경우
자, 그럼 KL divergence는 어떻게 두 분포사이의 거리를 측정할까요?
$$\mathrm{KL}\left(\mathbb{P}_{\theta} \| \mathbb{P}_{0}\right)=\int_{\left\{x: P_{\theta}(x) \neq 0\right\}} \log \left(\frac{P_{\theta}(x)}{P_{0}(x)}\right) P_{\theta}(x) \mu(d x)$$
$P_\theta>0$ 인 곳에서, $P_{0}(x)=0$ 이 되니까 아래와 같이 쓸수 있겠네요.
$$\log \left(\frac{P_{\theta}(x)}{P_{0}(x)}\right)=\infty$$
그럼 KL은 아래와 같이 계산됩니다.
$$\mathrm{KL}\left(\mathbb{P}_{\theta} \| \mathbb{P}_{0}\right)=\int \infty \cdot P_{\theta}(x) \mu(d x)=\infty$$
즉, $KL$ 값은 무한대의 값을 가지게 됩니다.
$\theta$ 가 0 이아닌 어떤 값이든, 모든 상황에서 무한대의 값을 가지게 되죠.
$$\mathrm{KL}\left(\mathbb{P}_{0}\| \mathbb{P}_{\theta} \right)=\mathrm{KL}\left(\mathbb{P}_{0} \| \mathbb{P}_{\infty}\right)=\left\{\begin{array}{ll}\infty & : \theta \neq 0 \\0 & : \theta=0\end{array}\right.$$
JSD의 경우
이 경우는 매우 간단합니다. 한번 보시죠.
$$\begin{aligned}\mathrm{KL}\left(\mathbb{P}_{0} \| \mathbb{P}_{m}\right)=\int_{P_{0} \neq 0} \log \left(\frac{P_{0}(x)}{P_{0}(x) / 2}\right) P_{0}(x) \mu(d x)=\log 2 \\\mathrm{KL}\left(\mathbb{P}_{\theta} \| \mathbb{P}_{m}\right)=\int_{P_{\theta} \neq 0} \log \left(\frac{P_{\theta}(x)}{P_{\theta}(x) / 2}\right) P_{\theta}(x) \mu(d x)=\log 2\end{aligned}$$
그러므로 $\theta\neq0$ 이면 JS는 $\text{log}2$ 의 값을 가지게 됩니다. 따라서
$$\operatorname{JS}\left(\mathbb{P}_{\theta}, \mathbb{P}_{0}\right)=\left\{\begin{array}{ll}\log 2 & : \theta \neq 0 \\0 & : \theta=0\end{array}\right.$$
가 된다는 것이죠. 따라서 마찬가지로 $\theta$ 의 값과 상관없이 상항 같은 상수값을 나타내게됩니다.
GAN에서의 의미
이는 GAN을 학습하는데 큰 문제가 됩니다. Loss Function은 가까우면 가깝다고, 멀면 멀다고 명확히 말을 해주어야 이에 따른 gradient를 계산할 수 있습니다. 하지만 두 분포의 SUPP이 겹치지 않는다면 '두 분포가 완전히 다르다.' 라는 정보만 줄 뿐 어떻게 가깝게 만들지에 대한 정보 즉 gradient를 계산할 수 없다는 뜻입니다.
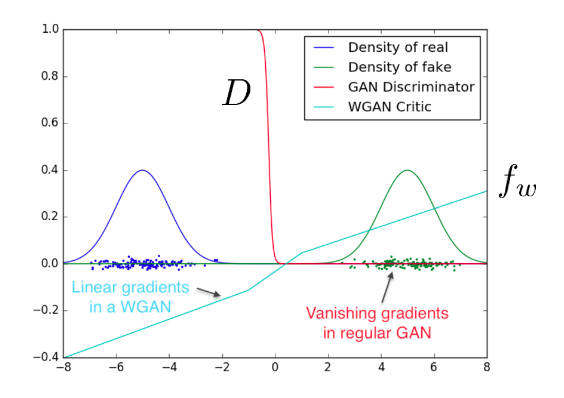
즉, D가 너무 깐깐하게 두 분포를 판단해서, 만약 두 분포가 겹치지 않는다면 두분포를 어떻게 가깝게 만들지에 대한 gradient를 계산할 수 없게 된다는 거죠.
이는 사실 일만적으로 이미지 생성과 같은 높은 dimension의 문제를 푸는 GAN에서는 이러한 분포가 겹치지 않는 문제가 더 심하게 발상할 것이기 때문에 GAN의 학습 성능이 떨어지는 등 꽤 크리티컬한 문제로 다가올 것이었습니다.
이 문제를 해결하러 왔다.
이 문제를 해결하기 위해서 2가지 방법을 소개해드리도록 하겠습니다.
- 분포를 건드리는 방법
- 분포의 거리 측정 방식을 개선하는 방법
당연히 우리가 앞으로 할 짓은 후자입니다만, 전자 쪽은 매우 간단하고 직관적으로 이해가 쉬우니까 한번 보고 가실께요.
노이즈를 통한 해결
Support가 겹치지 않는 것이 문제였습니다. 때문에 기존의 이미지에 노이즈 n을 추가해주면서 아래 그림처럼 두 분포의 Support영역을 넓혀 겹칠수 있도록 만들어주는 것입니다. 이렇게 두 분포를 겹치게 만들어주면 JSD를 사용해서 문제를 해결할 수 있습니다.

하지만 이러한 해결방법은 생성된 이미지가 굉장히 흐릿하게 나오는 등 문제가 발생하는 등 성능이 좋지 않게 나왔다고 합니다.
JSD가 아닌 다른 형태의 거리 측정 방식 사용
JSD는 두 분포가 겹치지 않을 때 상수가 나와 gradient를 계산하기 힘든 문제가 있었습니다.
따라서 저자는 분포가 겹치지 않아도 두 분포의 거리를 측정할 수 있는 방법인 Earth Mover Distance를 사용할 것을 제안합니다. 그리고 이제부터가 WGAN의 시작이죠.
WGAN은 다음 포스팅에서 다루도록 하겠습니다. 길이 너무 길어져서 여기서 한번 끊고 가도록 하겠습니다.
Reference
- (Paper) Goodfellow, Ian J., et al. "Generative adversarial networks." arXiv preprint arXiv:1406.2661 (2014).
- (Paper) Goodfellow, Ian. "Nips 2016 tutorial: Generative adversarial networks." arXiv preprint arXiv:1701.00160 (2016).
- (Paper) Arjovsky, Martin, Soumith Chintala, and Léon Bottou. "Wasserstein generative adversarial networks." International conference on machine learning. PMLR, 2017.
- PR-001: Generative adversarial nets by Jaejun Yoo (2017/4/13)
- General introduction of GAN
- 1시간만에 GAN(Generative Adversarial Network) 완전 정복하기
- GAN, WGAN, WGAN-GP
- WGAN
- WGAN의 수학 이해하기
- WGAN-GP이해하기
- WGAN-GP 소스코드
- Wasserstein-gan-i
- GAN ; WGAN & WGAN-gp
- GAN with Mathematics
'ML > 논문리뷰' 카테고리의 다른 글
| [논문 정리] GAN에 대해서 알아보자 (1) - 개념, 알고리즘, 소스코드 분석 (6) | 2021.04.03 |
|---|---|
| [논문 정리] AdaIN을 제대로 이해해보자 (0) | 2021.03.17 |
| [논문 번역] 불친절한 AdaIN 논문 읽기 (Arbitrary Style Transfer in Real-Time With Adaptive Instance Normalization) (0) | 2021.03.10 |
